FFT前置知识
FT和DFT
傅里叶变换FT(fourier transform)用于将时域信号$x(t)$和频域信号$X(f)$之间变换,公式如下所示:
对于计算机系统中,无法处理连续的过程,因此离散化为离散傅里叶变换DFT(Discrete Fourier Transform):
取$W_N = e^{-\frac{2\pi}{N}j}$,可将DFT改写为以下公式:
DFT改进(削减计算量)
首先分析原始公式的计算量,取一个8点DFT算法,对于一个点:
- 需要复数乘法N次,每次复数乘法由四次实数乘法和两次实数加法实现
- 需要复数加法N-1次,每次复数加法由两次实数加法构成
因此,对于一个点,需要实数乘法共4N次,实数加法共(2N-2+2N)=4N-2次。削减计算量的主要重点在$W_N$上,使用欧拉公式有:
考虑$W_N^{k+\frac{N}{2}}$的情况,有以下公式:
同理有$W_N^{k+N} = W_N$,因此以一个4点DFT为例,有以下公式:
可减少所需要的复数乘法的次数,进而减少对应的实数乘法和加法的数量
FFT
基2FFT
基2FFT指点数为$2^n$的FFT变换,取$N = 2^n$的FFT变换如下所示:
将一个N点的FFT分解为两个FFT,一个为奇数项的FFT,另一个为偶数项的FFT。对于$W_N^{nk}$而言,考虑以下变化:
带入上式,有以下:
取$FFT1(k) = \sum\limits^{\frac{N}{2}-1}{n=0}x(2n)W{\frac{N}{2}}^{kn} $和$FFT_2(k) = \sum\limits^{\frac{N}{2}-1}{n=0}x(2n+1)W_{\frac{N}{2}}^{nk}$分别是两个长度为$\frac{N}{2}$的FFT运算,有:
上述有$n < \frac{N}{2}$,考虑后半段结果,有:
同理有$FFT_2(k+\frac{N}{2}) = FFT_2(k)$,因此当$n \geq \frac{N}{2}$时,考虑$W_N$的周期性,有:
综上所述对于一个N点的FFT运算,有
其中,$FFT_1$为对偶数序列的$\frac{N}{2}$点FFT;$FFT_2$为对应奇数序列的$\frac{N}{2}$点FFT。该操作将一个N点FFT分解为两个$\frac{N}{2}$点的FFT。
蝶形运算
蝶形运算为一个二输入二输出的运算,公式如下所示:
其中$X_1,X_2$为两个输入;$Y_1,Y_2$为两个输出;W为权值,均为复数。蝶形运算可以用于映射基2FFT,首先考虑2点FFT,两点FFT公式如下所示:
因此可以使用一个蝶形运算实现,权值为$W_2^k$,现考虑一个4点FFT,首先将其分解为2个两点FFT,分解的公式为
分解步骤也可以用蝶形运算实现,因此整体运算如下图所示:
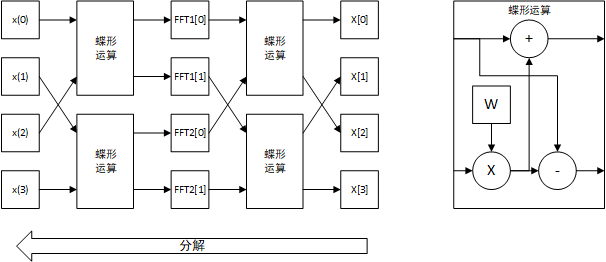
更多点数的FFT可以类似的进行,即不断分解为长度为一半的奇偶序列的FFT变换分层实现。
