算法基础
EIE(Efficient Inference Engine)的算法基础是一种被称为Deep Compression的神经网络压缩算法。EIE可以说是为Deep Compression量身定制的硬件,Deep Compression的算法流程如下所示:
- 剪枝:将小于某个阈值的权值直接置为0,这一操作引入权值的稀疏性
- 量化:这里的量化是一种非线性量化,通过k近邻类聚算法确定量化中心和量化间隔
- 编码:原文中使用霍夫曼编码压缩权值的存储,EIE中使用CSC压缩存储方式
Deep Compression压缩
Deep Compression压缩分为剪枝、量化和编码操作。其中剪枝为对所有权值做以下操作:
其中T为剪枝阈值,该步骤将所有小于剪枝阈值T的权值置为0,引入了权值的稀疏性。原文中对于VGG结构的剪枝后,卷积层的非零参数量一般还剩原参数量的30%~60%中,全连接层的非零参数量一般仅剩5%以下,由于全连接层参数占参数的主要部分,因此全网络的非零参数量仅剩下原有的7.5%。考虑VGG是比较容易产生冗余的网络,因此对其他网络的剪枝效果可能差于VGG网络。剪枝阈值T在剪枝过程中为超参数,需要综合考虑剪枝效果和剪枝后网络的性能表现多次试验确定。
量化操作为对于每个层,使用k-近邻类聚算法类聚。类聚算法产生指定数量的类聚中心,所有属于某一类的权值都被直接赋予类聚中心的值。随后使用修改过的优化算法运行一定轮数的训练,调整类聚中心的值(权值从属关系不改变),具体过程参见Deep Compression论文,这里仅考虑结果,进行完量化后,每一层的权值张量变为一个同形状的标号张量和一个解码表。标号张量标记每个位置的元素属于的类别,一般仅有2~5bit(即分为4~32类);解码表标记每个类别的数据,如下图所示:
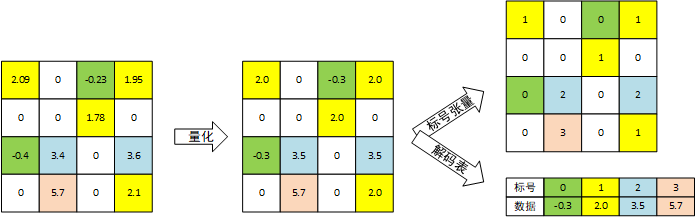
现在考虑量化对实现的影响。原有的高精度权值张量(取$D_H$bit)的非零参数量为M,则需要的存储空间为$M \times D_H$bit。量化后权值张量改为标号张量,标号的位数一般远远低于权值数据,取为$D_L$,需要存储空间为$M \times D_L$;另考虑编码表,编码表需要的bit数为$2^{D_L} \times D_H$。则量化后权值需要的存储空间占原有比例为:
$D_L$一般来说仅有5bit(VGG网络),因此有$M >> 2^{D_L}$,则可以发现将权值的存储空间降低到$\frac{5}{32} = 15.625\%$,有效的缓解了存储瓶颈。但是权值使用时,需要根据标号张量中的标号从编码表中查询权值,再将其与输入进行运算,比原有矩阵直接运算多一步查询,需要通过硬件查询。
Deep Compression论文中为了进一步压缩权值的存储,在量化后使用霍夫曼编码压缩矩阵的存储。EIE为了方便的硬件实现,使用CSC方法压缩稀疏权值矩阵。
CSC稀疏矩阵表示
CSC(compressed sparse column)为一种稀疏矩阵的表示方法,其将一个稀疏矩阵压缩表示为三个向量。首先考虑向量的压缩方法,每个稀疏向量被压缩为两个非稀疏向量,如下所示的向量:
将其压缩为两个长度相等的向量,第一个向量为按顺序排列的所有的非稀疏元素,第二个向量为对应位置的非稀疏元素与前面一个非稀疏元素中间的0数量,上述向量压缩完成如下所示:
u为非零元素,z为两个非零元素之间0的数量。例如$v[0]=1,z[0]=2$表示第一个非0元素为1,该元素之前有2个零;$v[1]=2,z[1]=0$表示第二个非0元素为2,该元素之前没有0(原向量中为$[0,0,1,2,…$)。由于这里的z向量使用的为int4类型数据,因此第三个非零数据3之前的18个零超出了表示范围,因此在v中添加一个0元素,即其中$v[2]=0,z[2]=15$表示第三个数据为0,之前有15个0。这个数据并不是非零数据,是为了能使用int4表示18而额外补充的数据。之后的$v[3]=3,z[3]=2$为要表示的数据3,之前有2个零,和前一条一起表示间隔18个零的情况,如下图所示:

随后考虑矩阵的表示方法,CSC稀疏表示将矩阵的每一列视为一个向量进行压缩,每一列都产生一个v向量和一个z向量,第i列产生的向量$v_i$和$z_i$向量的长度和其他列均可能不同。将每一列的v向量按列号依次连接,z向量按列号依次连接,获得矩阵的v和z向量,为了区分不同列,额外引入u向量,u向量长度为列数加1,表示每一列的v或z向量在矩阵v和z向量中的位置,即第i列的v和z向量在矩阵的v和z向量的第$u[i]$个到第$u[i+1] - 1$元素之间,u[0]固定为0。如下图所示:
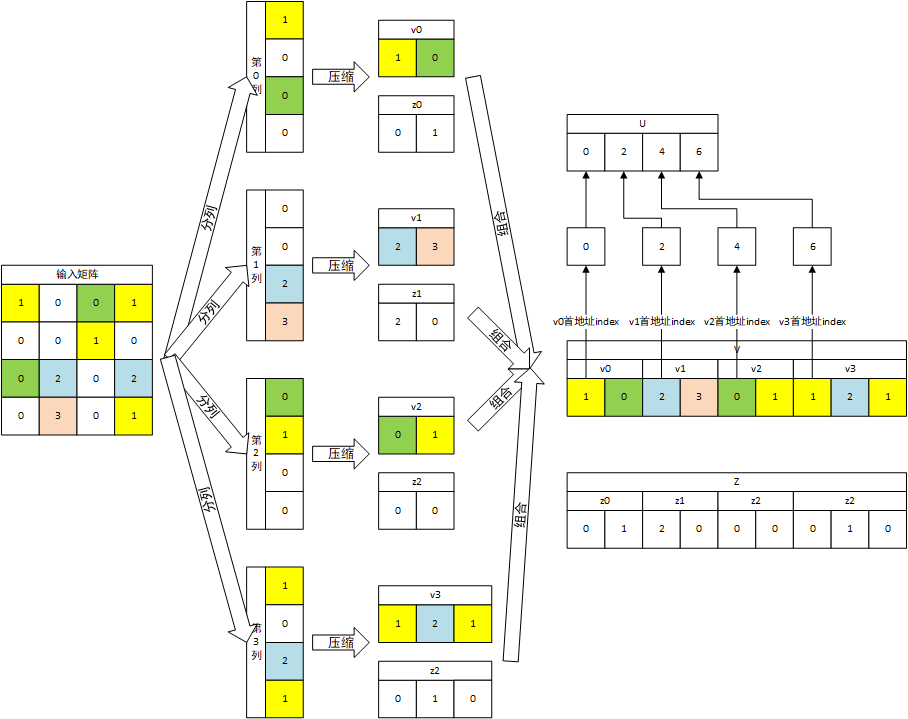
最终,一个稀疏矩阵将被压缩到三个向量U、V和Z中,该方式仅保存非零数据(为了表示超过Z限制额外引入的0除外),同时Z和U向量使用的数据类型一般比U小,因此可以有效的压缩稀疏矩阵。
EIE结构
PE结构
EIE(Efficient Inference Engine)作为一种Engine,主要作为加速器系统组件使用,因此论文中并未提出明确的系统架构,而是重点描述了其PE的结构,PE结构图如下:

PE按功能为以下几个部分:
- 蓝色底色部分为缓存部分,分布缓存了CSC格式表示矩阵方法下的U、V和Z向量以及Deep Compression产生的解码表和产生的部分和输出数据。
- 紫色底色部分为标号处理部分,标号累加为一个累加器,通过累加一个向量CSC表示中之前的元素的z部分产生该元素在向量中的实际绝对位置;列地址生成从矩阵从U向量中获取某一列的数据在V和Z向量中的起始和结束位置。
- 橙色底色部分为算数运算部分,输入数据和解码后的权值相乘并和之前的结构相加,结果保存在输出缓存中,当运算完成时,通过ReLu单元激活后输出。
该PE如何映射运算将在后续章节[算法映射]中表述。
CSC编码器
PE运算产生的结果并不是CSC方法表示。一般来说,在ReLU函数之前的输出数据并不具有稀疏性,但是ReLU函数将所有负数输出置为0,引入了输入\输出数据的稀疏性,因此需要将输出数据进行CSC编码,CSC编码器结构如下所示:
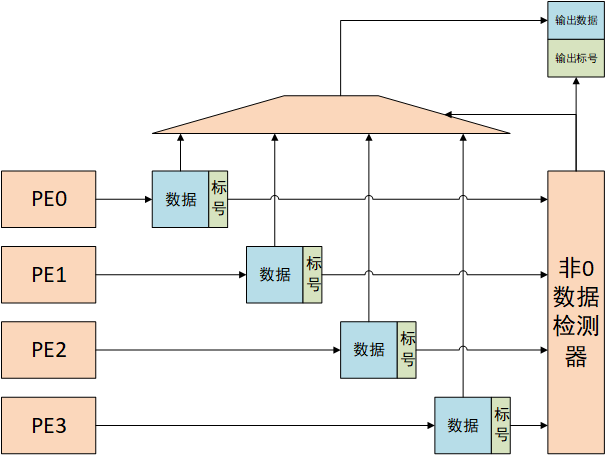
论文中PE以4个一组,每个PE输出一个输出数据及其绝对标号,非零数据检测器从PE0的输出数据开始依次检测,若发现非0数据,则通过绝对标号计算CSC格式的相对标号,同时输出器数据和相对标号,实现CSC编码。
算法映射
矩阵-向量乘法
原论文中以4个PE为一组,计算矩阵乘法。输入权值和输入数据以下图为例:
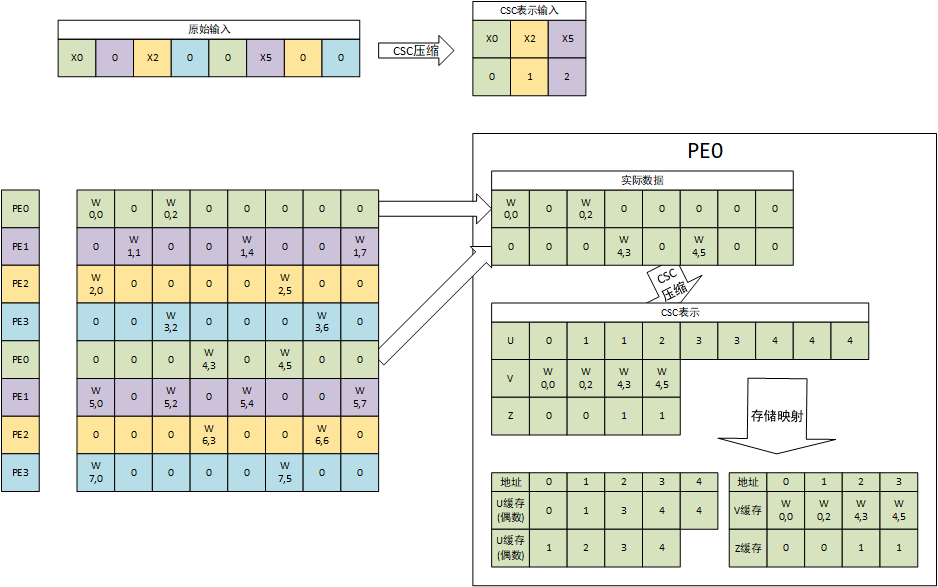
矩阵乘法计算的目标为:
上图中,有a=8、b=8。权值矩阵的第i行数据保存在标号为$i \% 4$的PE中并由该PE负责计算。第i个PE的所有权值行向量顺序堆叠组成一个新权值矩阵$W_i,W \in R^{(a//4) \times b}$,这里新权值矩阵为2行。标号为i的PE中存储的是新权值矩阵$W_i$的CSC表示。
EIE映射算法的原理如下图所示,综合考虑输入数据和权值的稀疏性,将矩阵-向量乘法分解为多个向量相乘,当且仅当对应位置上的元素均不为0时才进行计算,因此可以减少很多0之间的运算。
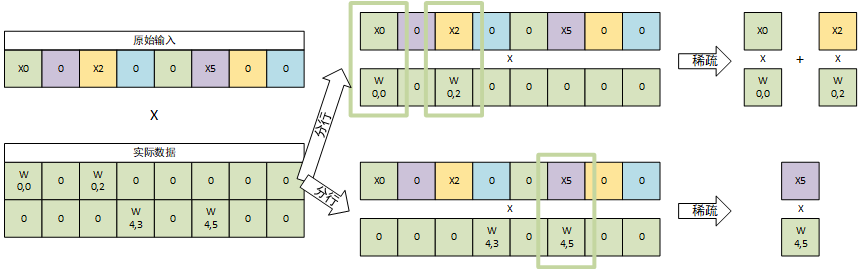
EIE的PE输入为一个CSC格式压缩的稀疏向量,将每个元素的数据和标号(v和z)依次输入数据队列和标号队列。处理一个数据时,从数据队列中取出数据D并从标号队列中取出标号$I_z$,标号$I_z$通过标号累加器变为向量的绝对坐标I。以上图中所述第一个数据X0为例,其相z元素为0,即之前没有0,因此X0的绝对位置为0。输入向量CSC格式累加过程如下所示:
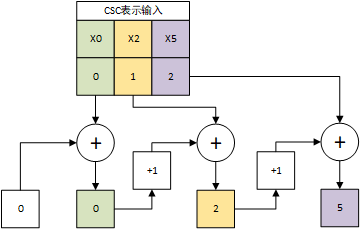
随后通过$I//2$查询奇数U缓存,$I // 2 + I \%2$查询偶数缓存。分别从偶数U缓存和奇数U缓存中获取地址各一个:
- 若I为奇数,则从奇数缓存中读取的数据为起始地址$U_s$,从偶数缓存中读取的数据为结束地址$U_e$
- 若I为偶数,则从偶数缓存中读取的数据为起始地址$U_s$,从奇数缓存中读取的数据为结束地址$U_e$
对于X0而言,对应绝对位置为0,读出起始地址为0,结束地址为1;对于X2,读出起始地址为1,结束地址为2;对于X5,读取起始地址为3,读取终止地址为4。对于$Us = U_e$的情况,说明该输入数据对应的列无非0数据,可直接跳过该输入数据的处理过程。随后使用$U_s$和$U_e$之间的值(不包括$U_e$,即$[U_s,U_e)$)从V缓存和Z缓存中读取权值。对于X0,读出权值$W{0,0}$和相对位置0,对于X2,读取权值$W{0,2}$和相对位置0;对于X5,读取权值$W{4,5}$和相对位置1。根据这些权值从编码表中查询真实权值。相对位置进行与输入相同的权值累加计算真实权值WI,计算结果分别为0、0和1。
随后输入数据与读出的真实权值依次相乘,相乘的结果与输出缓存中位置为WI的数据累加,过程如下所示:
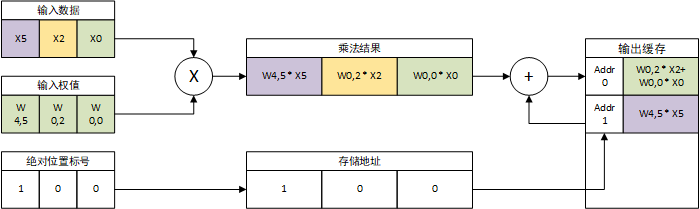
累加完成后,输出缓存每个地址存储的就是对应绝对位置的输出结果,完成矩阵-向量乘法映射。
卷积映射
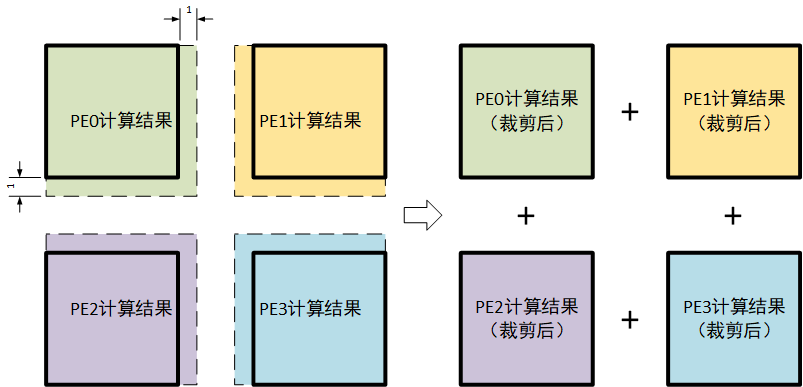
卷积映射在原论文中没有提到,一下为基于结构对映射卷积方式的猜测,其映射卷积的方式可能为将卷积拆分为多个矩阵乘法实现,如下图所示:
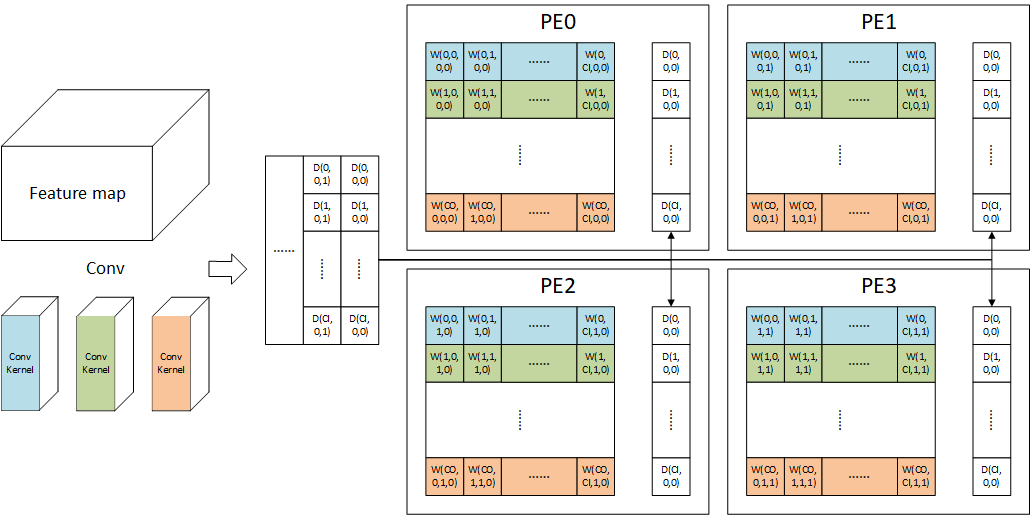
PE的输入为广播输入,因此所有PE的输入数据必须相同,而所有权值均为本地存储,因此权值应当不在PE之间交换,由上推测出卷积的映射方法应当将一个$K \times K$的卷积变为$K \times K$个$1 \times 1$卷积实现。上图举出了一种$2 \times 2$卷积在EIE上实现的可能方案。每个PE计算一个输出通道为CO+1,输入通道为CI+1的$1 \times 1$卷积,所有PE计算完成后,将结果错位相加即可获得$2 \times 2$卷积的计算结果,错位相加过程如下所示: