简介
DianNao系列是中科院计算所推出的系列机器学习加速器,包括以下四个成员:
- DianNao:神经网络加速器,DianNao系列的开山之作。
- DaDianNao:神经网络“超级计算机”,DianNao的多核升级版本
- ShiDianNao:机器视觉专用加速器,集成了视频处理部分
- PuDianNao:机器学习加速器,DianNao系列收山之作,可支持7种机器学习算法
DianNao系列相比于其他神经网络加速器,除了关心运算的实现外,更关心存储的优化。
整体架构
DianNao系列的整体架构比较类似,均分为以下三个部分:
- 运算核心:完成对应的运算加速功能
- 缓存:缓存输入输出数据与参数,减小访存带宽需求
- 控制:协调运算核心和缓存的工作
前三代(DianNao,DaDianNao,ShiDianNao)的整体架构如下图所示:
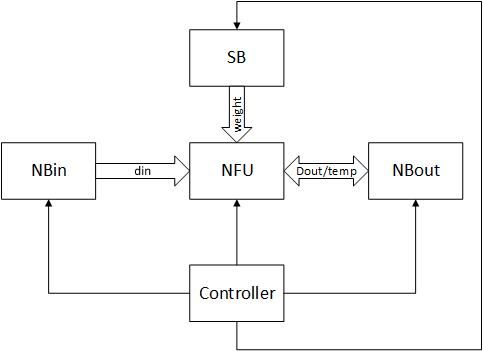
其中:
- NBin,NBout和SB:均为存储器,分别用于存储输入数据,输出数据或临时数据和参数
- NFU:运算核心,用于完成神经网络相关的运算
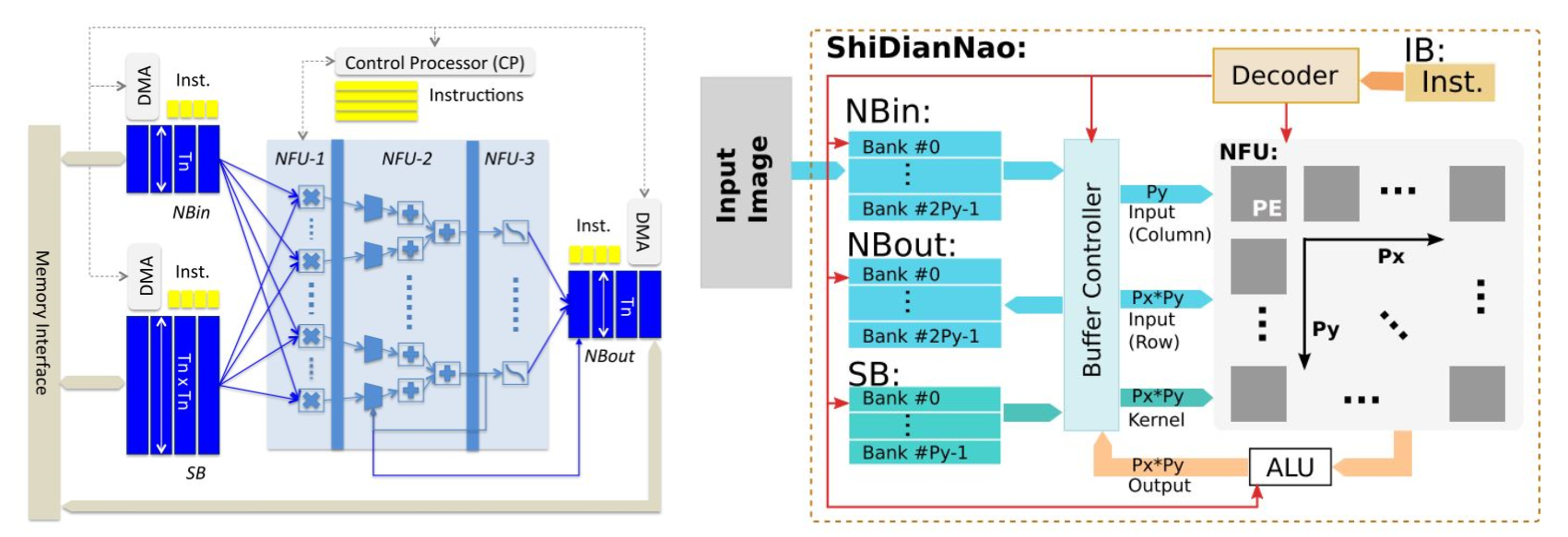
以下为原论文中所绘制的架构图(左图为DianNao/DaDianNao,右图为ShiDianNao):
最后一代PuDianNao为了适应更多的机器学习算法(PuDianNao不专门为神经网络设计),抛弃了按功能分别缓存的方法,转而使用按重用频率缓存,因此架构上发生了一些变化,如下图所示:
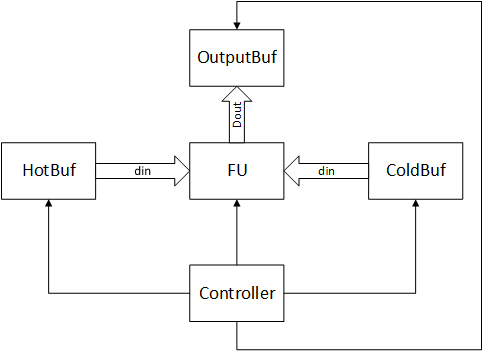
其中:
- HotBuf,ColdBuf:输入数据缓存,分别用于存储频繁重用和重用时间间隔较长的输入数据
- OutBuf:输出数据缓存,用于存储输出数据
- FU:功能模块,完成机器学习相关运算
- Controller:控制核心,协调存储器和功能模块的工作
原论文中绘制的系统结构图如下所示:
运算模块
运算模块用于完成待加速的运算,是加速器的核心部分之一。
运算分析
DianNao系列的论文每一篇都会花大量的篇幅阐述运算分析部分,这对学习者来说非常友好。
DianNao与DaDianNao
这两个系列支持的神经网络计算类型较为基础,论文中概括,要想实现卷积神经网络,需要实现以下几种操作:
- 卷积运算:$out(x,y)^{fo} = \sum \limits{f_i = 0}^{K{if}} \sum \limits{k_x = 0}^{K_x} \sum\limits{ky = 0}^{K_y} w{f_i,f_o}(k_x,k_y) \times in(x+k_x,y+k_y)^{f_i}$
- 池化运算:$out(x,y)^f = max_{0 \leq k_x \leq K_x,0 \leq k_y \leq K_y} in(x+k_x,y+k_y)^f$
- LRN(区域响应标准化,当时批标准化还未流行):$out(x,y)^f = \cfrac{in(x,y)^f}{(c + \alpha \sum \limits_{g=max(0,f-k/2)}^{min(N_f,f+k/2)}(a(x,y)^g)^2)^{\beta}}$
- 矩阵乘:$out(j) = t(\sum\limits^{Ni}{i = 0} w_{ij} \cdot in(i))$
其中,DianNao未实现LRN功能,该功能在DaDianNao中才实现。另外,DaDianNao支持神经网络的训练,其训练过程所需要的运算,基本与测试过程基本相同。
ShiDianNao
ShiDianNao除了支持DianNao所支持的操作外,对于标准化,还支持LCN(局部对比度归一化):
PuDianNao
PuDianNao支持7种机器学习算法:神经网络,线性模型,支持向量机,决策树,朴素贝叶斯,K临近和K类聚,所需要支持的运算较多,因此PuDianNao的运算分析主要集中在存储方面,其运算核心的设计中说明PuDianNao支持的运算主要有:向量点乘,距离计算,计数,排序和非线性函数。其他未覆盖的计算使用ALU实现。
运算模块设计
DianNao
DianNao的运算模块奠定了DianNao系列运算模块的主基调。结构图如下所示:
运算模块分为三级流水线:
- NFU-1:乘法器阵列,16bit定点数乘法器,1位符号位,5位整数位,10位小数位
- NFU-2:加法树/最大值树,将乘法器所得的结果累加或取最大值,可选的与上一次/部分和累加。这一部分的结尾处有寄存器结构,可以存储这一次运算的部分和。
- NFU-3:非线性激活函数,该部分由分段线性近似实现非线性函数
当需要实现向量相乘和卷积运算时,使用NFU-1完成对应位置元素相乘,NFU-2完成相乘结果相加,最后由NFU-3完成激活函数映射。完成池化运算时,使用NFU-2完成多个元素取最大值或取平均值运算。由此分析,尽管该运算模块非常简单,也覆盖了神经网络所需要的大部分运算(LRN在DianNao中未实现)
DaDianNao
DaDianNao的运算单元NFU与DianNao基本相同,最大的区别是为了完成训练任务多加了几条数据通路,且配置更加灵活。NFU的尺寸为16x16,即16个输出神经元,每个输出神经元有16个输入(输入端需要一次提供256个数据)。同时,NFU可以可选的跳过一些步骤以达到灵活可配置的功能。DaDianNao的NFU结构如下所示:
ShiDianNao
ShiDianNao是DianNao系列中唯一一个考虑运算单元级数据重用的加速器,也是唯一使用二维运算阵列的加速器,其加速器的运算阵列结构如下所示:
ShiDianNao的运算阵列为2D格点结构,对于每一个运算单元(节点)而言,运算所使用的参数统一来源于Kernel,而参与运算的数据则可能来自于:
- 数据缓存NBin
- 下方的节点
- 右侧的节点
下图为每个运算单元的结构(左)和抽象结构(右):
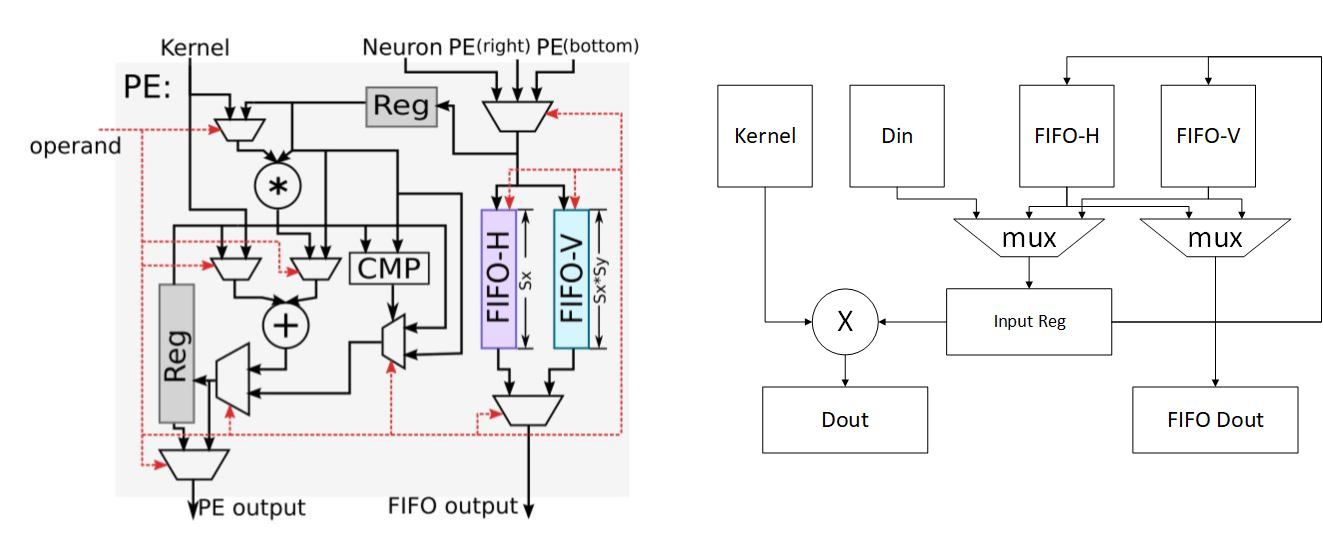
该计算节点的功能包括转发数据和进行计算:
- 转发数据:每个数据可来源于右侧节点,下方节点和NBin,根据控制信号选择其中一个存储到输入寄存器中,且根据控制信号可选的将其存储到FIFO-H和FIFO-V中。同时根据控制信号选择FIFO-H和FIFO-V中的信号从FIFO output端口输出
- 进行计算:根据控制信号进行计算,包括相加,累加,乘加和比较等,并将结果存储到输出寄存器中,并根据控制信号选择寄存器或计算结果输出到PE output端口。
对于计算功能,根据上文的结构图,可以发现,PE支持的运算有:kernel和输入数据相乘并与输出寄存器数据相加(乘加),输入数据与输出寄存器数据取最大或最小(应用于池化),kernel与输入数据相加(向量加法),输入数据与输出寄存器数据相加(累加)等。
PuDianNao
PuDianNao的运算单元是电脑系列中唯一一个异构的,除了有MLU(机器学习单元)外,还有一个ALU用于处理通用运算和MLU无法处理的运算,其运算单元(左)和MLU(右)结构如下图所示:
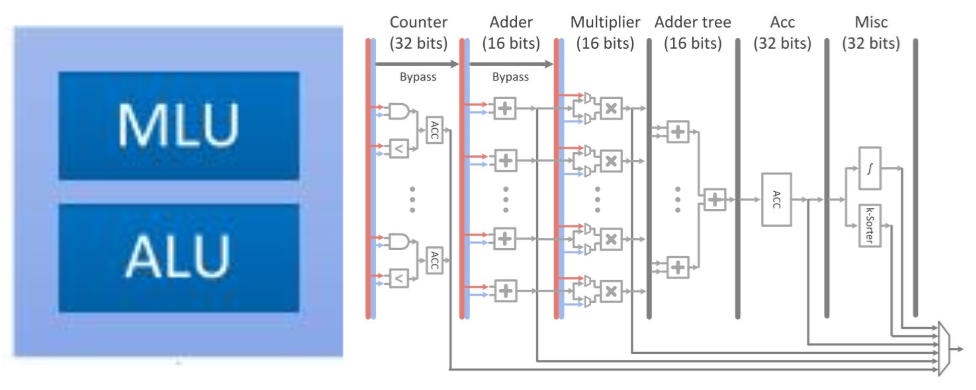
MLU分为6层:
- 计数层/比较层:这一层的处理为两个数按位与或比较大小,结果将被累加,这一层可以单独输出且可以被bypass
- 加法层:这一层为两个输入对应相加,这一层可以单独输出且可以被bypass
- 乘法层:这一层为两个输入或上一层(加法层)结果对应位置相乘,可以单独输出
- 加法树层:将乘法层的结果累加
- 累加层:将上一层(加法树层)的结果累加,可以单独输出
- 特殊处理层:由一个分段线性逼近实现的非线性函数和k排序器(输出上一层输出中最小的输出)组成
该运算单元是DianNao系列中功能最多的单元,配置非常灵活。例如实现向量相乘(对应位置相乘后累加)时,弃用计数层,加法层,将数据从乘法层,加法树层和累加层流过即可实现。
存储
DianNao系列的存储的设计理念是分裂存储,这样有几个好处:
- 增大带宽:相同大小的单个存储器和多个存储器相比,多个存储器能提供更大的带宽
- 匹配位宽:有些数据对位宽的需求不同,将位宽需求不同的数据放在不同位宽的存储器中可以避免位宽浪费
DianNao与DaDianNao
DianNao和DaDianNao的存储设计基本相同,区别在于DaDianNao使用了片上eDRAM增大了片上存储的面积,下图为DaDianNao的存储部分,DianNao的存储部分类似,可以参考整体架构中DianNao的架构图:
存储被分裂为三个部分:
- NBin:用于存储输入数据,需要位宽$T_n$(一次处理所需的输入数量x每个输入位宽)
- NBout:用于存储部分和与最终运算结果,需要位宽$T_n$
- SB:用于存储权值,需要位宽$T_n \times T_n$
DianNao和DaDianNao的重用策略是重用输入数据即NBin中的数据。当需要NBin参与的运算全部完成后,NBin才会被覆盖。因此,在DaDianNao中,所有运算单元共享eDRAM实现的NBin和NBout(图中eDRAM router部分),但具有自己的SB缓存(每个节点有4个eDRAM)
ShiDianNao
ShiDianNao的存储比较有特色,由于其特殊性,并未采用DaDianNao的eDRAM组成超大片上存储。仅使用了288KB的SRAM,因此其存储组织更值得研究,下图为NBin缓存及其控制器的设计:
可以发现,每个存储器分裂为$2 \times P_y$个Bank,每个Bank的位宽是$P_x \times 16bit$。其中$P_y$为运算阵列的行数,$P_x$为计算阵列的列数,16bit为数据位宽。该存储器支持的读取方式有6种:
- 读bank0~bank$P_y-1$,共$P_y \times P_x \times 16bit$数据,可以填充计算阵列中每个节点。
- 读bank$P_y$~bank$2 \times P_y-1$,共$P_y \times P_x \times 16bit$数据,可以填充计算阵列中每个节点。
- 读取一个Bank,共$P_x \times 16bit$数据,可以填充计算阵列中的一行。
- 读取一个Bank中的一个数据(16bit)
- 读取每个Bank中指定间隔的数据,共$2 \times P_y \times 16bit$数据。
- 读取bank$P_y$~bank$2 \times P_y-1$中每个Bank中指定位置的数据,共$P_y \times 16bit$数据,可以填充计算阵列中的一列。
写方面,采用缓存-存储的方式,即现先待写入数据换存入output寄存器中,待全部运算单元完成运算后统一将数据从output寄存器中写入存储器。
PuDianNao
PuDianNao抛弃了按用途分裂存储器的方法,改为按重用频率分裂存储器。且其设计方法更贴近通用处理器CPU,以实现通用机器学习处理器。PuDianNao认为其能实现的7种机器学习算法在存储上分为两种:
第一种与k-NN(k-邻近算法)类似,每个数据的重用间隔(这一次使用和下一次使用之间的间隔数据数量)明确的类聚为几类。第二种与NB(朴素贝叶斯)类似,除了位置为1上的明显类聚外,数据重用间隔在一段上均有分布。因此PuDianNao实现三个片上存储,分别为:
- ColdBuffer:16KB,存储重用间隔较长的数据,位宽较小。
- HotBuffer:8KB,存储重用数据较少的数据,位宽较大。
- OutputBuffer:8KB,存储输出数据。
映射方法
映射方法指现有硬件加速器如何实现神经网络中的运算,包括卷积,池化和全连接层等。
DianNao与DaDianNao
由于DianNao和DaDianNao的论文中都没有明确阐述这两款加速器如何映射运算,因此以下内容均为个人推测
DianNao和DaDianNao的运算单元均为NFU,参考其设计,其功能描述如下:
向量内积与卷积
无论是向量内积还是卷积,其最终都是对应位置元素相乘再相加。都可以使用运算核心的MUL功能解决,即将NFU-2配置为加法树。在存储中,输入数据按[高度,宽度,通道数]维度排列,即先存储第一个数据位置的所有通道数据,再存储第二个数据位置的所有通道数据,以此类推。权值数据按[高度,宽度,输出通道数,输入通道数]排列。其实现图如下所示:
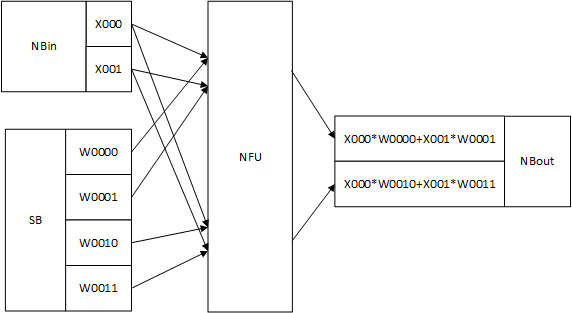
上图为一个$T_n = 2$的例子,其中数据含义如下所示:
| 标记 | 来源 | 说明 |
|---|---|---|
| X000 | 输入数据 | 数据位置(0,0),通道0数据 |
| X001 | 输入数据 | 数据位置(0,0),通道1数据 |
| W0000 | 参数 | 数据位置(0,0),通道0数据对应输出通道0的参数 |
| W0001 | 参数 | 数据位置(0,0),通道1数据对应输出通道0的参数 |
| W0010 | 参数 | 数据位置(0,0),通道0数据对应输出通道1的参数 |
| W0011 | 参数 | 数据位置(0,0),通道1数据对应输出通道1的参数 |
其实现的运算在卷积中如下所示:
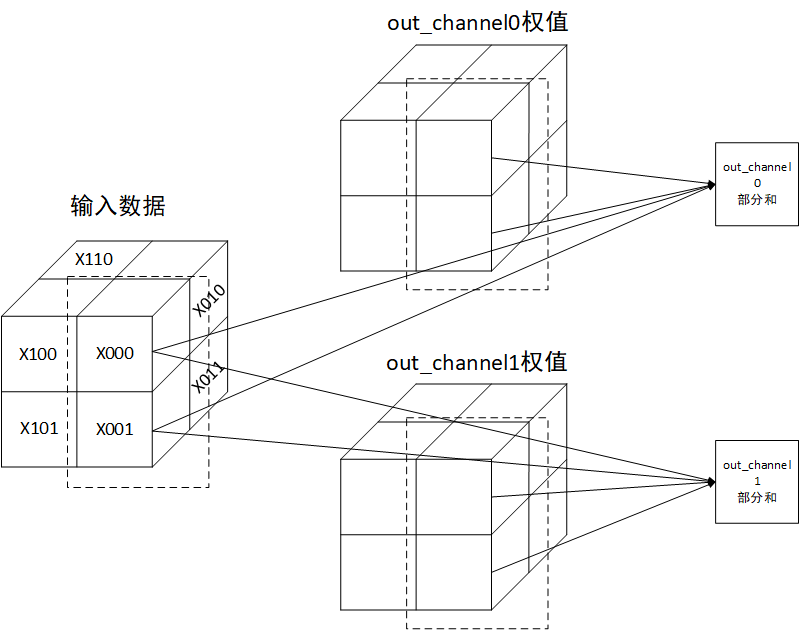
池化
实现池化层时,输入数据按[通道数,高度,宽度]排列,NFU-2被配置为取最大值树。
ShiDianNao
ShiDianNao由阵列实现卷积,池化,向量内积等操作,映射比较复杂。以下说明均使用$P_x=P_y=2$
卷积
ShiDianNao的每个节点的简化图形如下所示,以下说明将使用该图示:

实现卷积的第一步是初始化,将数据读入运算阵列,使用缓存读方式1或2:
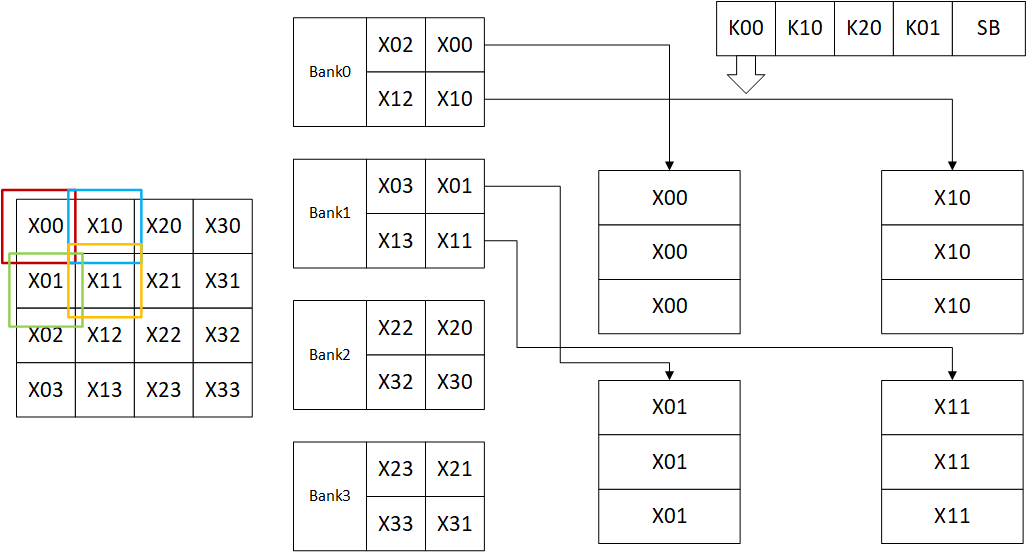
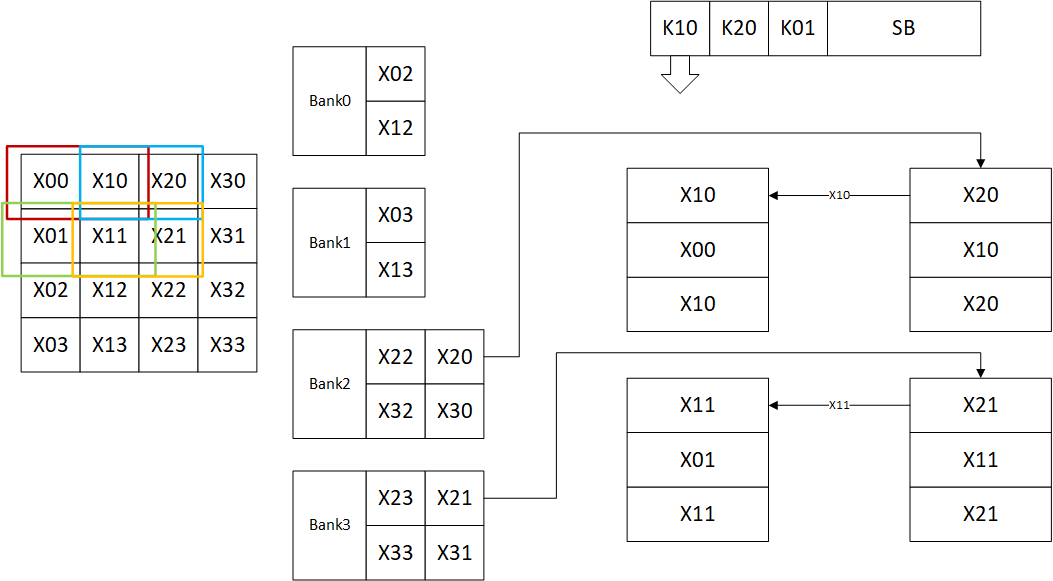
随后读Bank2和Bank3的第一个神经元,将其填充到运算阵列的右侧,同时输入数据右移,这等效的是标记参与运算的数据框向右扩展:
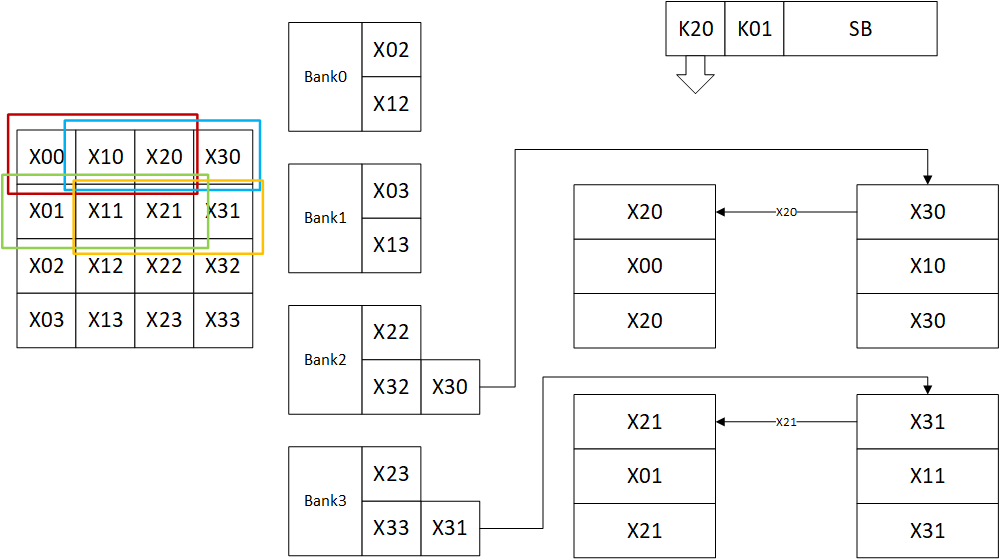
之后读Bank2和Bank3的第二个神经元,将其填充到运算阵列右侧,同时输入数据右移,这等效的是标记参与运算的数据框向右扩展:
随后读Bank1的两个神经元,将其填充到底部,同时数据上移,这等效标记参与运算的数据框向下扩展:
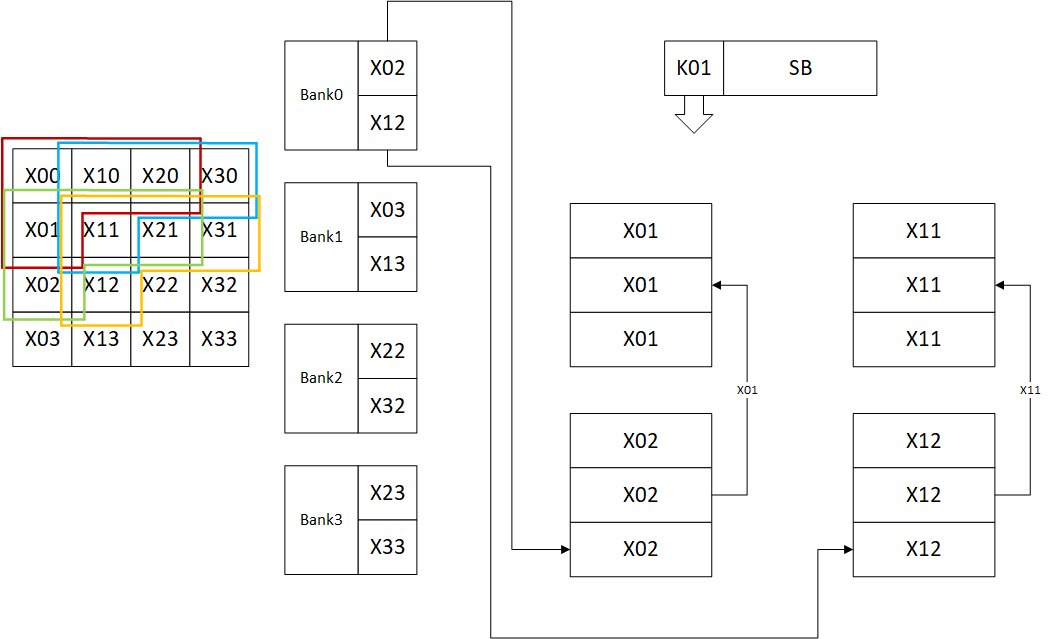
下表表示了每一个运算节点使用过的权值和数据:
| 坐标 | 参数=K00 | 参数=K10 | 参数=K20 | 参数=K01 |
|---|---|---|---|---|
| 0,0(左上) | X00 | X10 | X20 | X01 |
| 0,1(右上) | X10 | X20 | X30 | X11 |
| 1,0(左下) | X01 | X11 | X21 | X02 |
| 1,1(右下) | X11 | X21 | X31 | X12 |
注意上文中运算单元和SB的行为为原文中注明的,存储器行为为个人推断,此外,原文中的推断到此为止,理由为保持简洁,然而下一步的操作使用以上几步无法完全推测,原文中说明该复用方法可以节约44.4%的带宽,有$4 \times 9 \times 44.4\% = 16$,所以一共读了20次,图像中有16个数据,推测就是中心处被复用最多次的X11,X21,X12和X22。该部分说明的原图如下图所示:
池化
池化的映射方法与卷积类似,且由于池化的Stride一般不为1,因此需要注意的是FIFO-H和FIFO-V的深度不再是1。其中$S_x$和$S_y$分别是X方向和Y方向的Stride。
全连接层
矩阵乘法中,每个计算节点代表一个输出神经元,除非一个输出神经元的计算全部完成,否则不会进行下一个神经元的运算。与卷积不同的是,被广播的数据是输入数据而不是权值。因为在矩阵乘运算中,权值的数量多于数据且不被复用。每次运算分为以下几个步骤:
- 一个输入数据和$P_x \times P_y$个权值,每个计算节点接收一个数据和被广播的数据。
- 计算节点将输入数据和权值相乘后与之前的部分和积累。
- 当一个输出神经元的所有计算都完成后,将每个节点累积的结果缓存回片上存储中。
PuDianNao
PuDianNao的映射方法比较简单,由于较多的考虑了灵活性,因此使用类似软件的方式控制整个芯片。推测方法为:
- 控制模块控制DMA将指定数据从片外存储搬运到片上buufer中,并将其搬运到指定处理单元中
- 处理单元在控制模块控制下对数据进行处理
- DMA将结果从处理单元单元搬运到buffer中
